Las matemáticas pueden ser un verdadero quebradero de cabeza para los estudiantes. La parte de Análisis no es menos, y por eso hemos recogido los diferentes tipos de funciones matemáticas que existen y sus gráficas.
Funciones polinómicas
Son las más sencillas porque vienen definidas por un polinomio y su dominio es todo ℝ, es decir, cualquier número real. Dentro de las funciones polinómicas existen diferentes tipos:
- Función constante.
f(x) = k. Es la más sencilla de todas, ya que la gráfica de esta función es una recta horizontal paralela al eje X.

- Función polinómica de primer grado – lineal.
f(x) = mx + n. Estas funciones tienen como gráfica una recta con pendiente m, es decir, es una recta con inclinación.

La función constante es una función polinómica de primer grado cuando m = 0.
- Función polinómica de segundo grado – cuadrática.
f(x) = ax2 + bx + c. Son una continuación de las funciones polinómicas de primer grado. “a” no puede ser igual a 0 porque entonces se trataría de una función lineal. Su representación gráfica es una parábola, que bien puede ser cóncava o convexa. La función puede cortar al eje X en 0, 1 o 2 puntos.

- Función cúbica
f(x) = ax3 + bx2 + cx + d. Son una continuación de las funciones polinómicas de segundo grado, y “a” no puede ser 0 porque entonces se trataría de una función cuadrática. La representación gráfica de esta función es una especie de mezcla entre parábolas cóncavas y convexa, y puede cortar al eje X en 1, 2 o 3 puntos.

Funciones racionales
f(x) = donde q(x) ≠ 0.
q(x) no puede ser igual a 0. ¿Por qué? Porque el denominador sería 0, se anularía y nos encontraríamos con una indeterminación.
Al ser el dominio todos los números reales ℝ menos 0, la gráfica es una hipérbola. Se acerca asintóticamente a 0 por ambos ejes pero nunca llega a tocarlos.

Funciones exponenciales
f(x) = ax siendo a un número real ℝ positivo mayor que 0 (a>0) y a≠1.
La base de la función exponencial es siempre positiva. La gráfica es una función que crece o decrece indefinidamente, con mayor o menor curva.

Funciones logarítmicas
y = log a x, siendo a un real ℝ positivo (a>0) y a ≠ 1. Los logaritmos son la inversa de las exponenciales.
La gráfica siempre corta al eje X en (1,0). ¿Por qué? Porque el logaritmo de cualquier base si x = 1 es igual a 0 (loga1=0).
Presenta una asíntota con respecto al eje Y, es decir, se acerca indefinidamente pero nunca llega a cortar al eje Y.

Funciones definidas a trozos
La función presenta diferentes expresiones matemáticas dependiendo del intervalo en el que se encuentre x. Por tanto, la gráfica depende de dichas expresiones y es diferente en cada intervalo del dominio de f(x).
Funciones trigonométricas
Estas funciones están asociadas a razones trigonométricas. Existen 6 tipos y cada una tiene su propia gráfica.
- Seno.
La función del seno tiene un periodo de 360º (2π radianes), lo que significa que se repetirá en cada periodo.

- Coseno.
La función del coseno tiene un periodo de 360º (2π radianes), lo que significa que se repetirá en cada periodo.
- Tangente.
La función de la tangente tiene un periodo de 180º (π radianes). En un periodo se repite 2 veces.

- Cosecante
La función de la cosecante tiene un periodo de 360º (2π radianes), lo que significa que se repetirá en cada periodo.
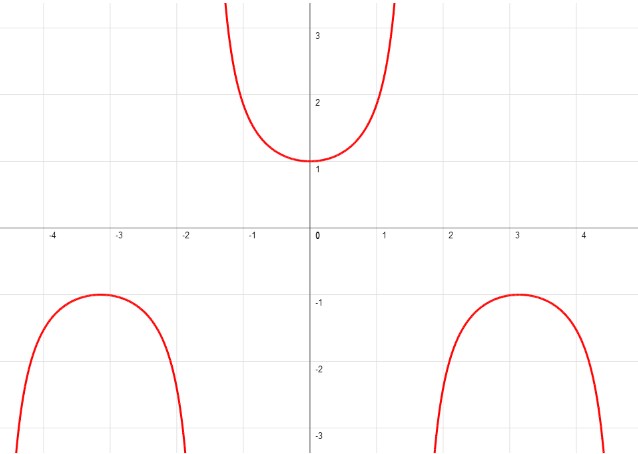
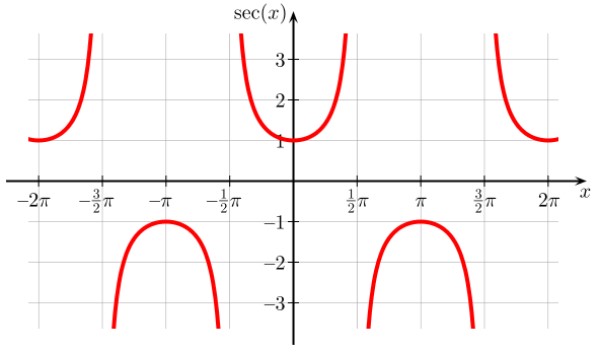
- Secante.
La función de la secante tiene un periodo de 360º (2π radianes), lo que significa que se repetirá en cada periodo.
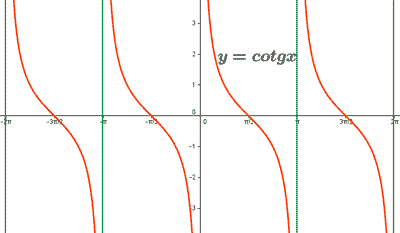
- Cotangente
La función de la cotangente tiene un periodo de 180º (π radianes). En un periodo se repite 2 veces.